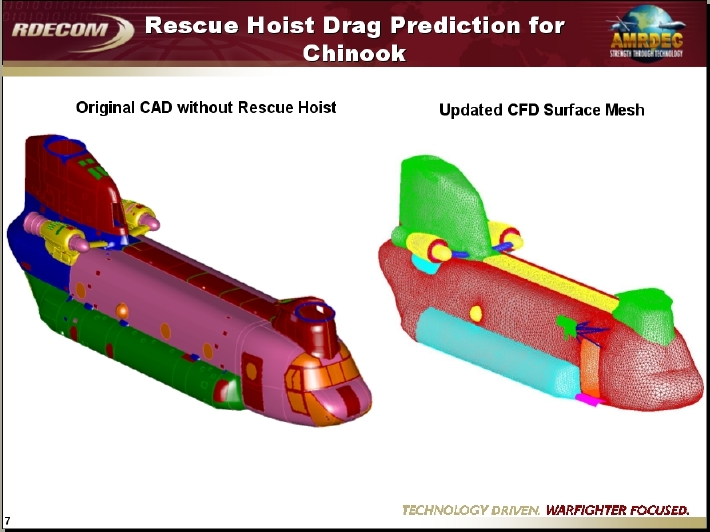
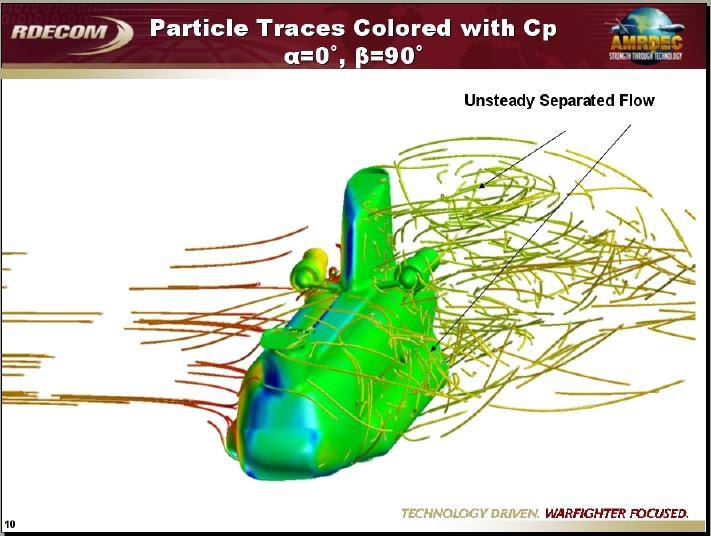
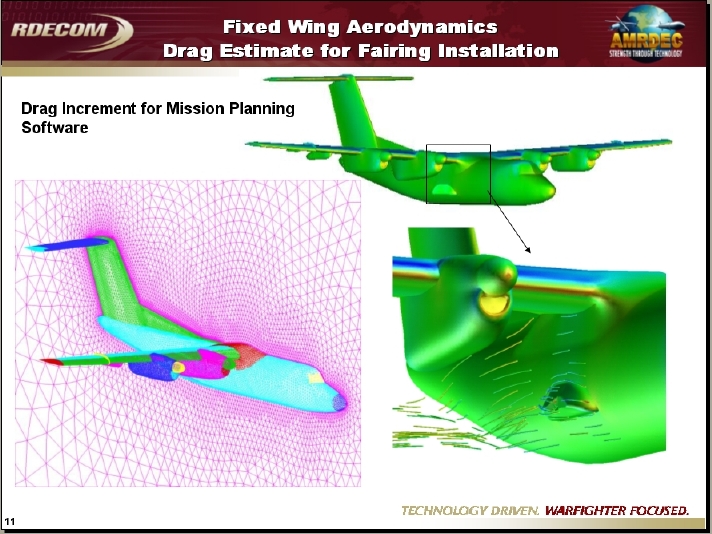
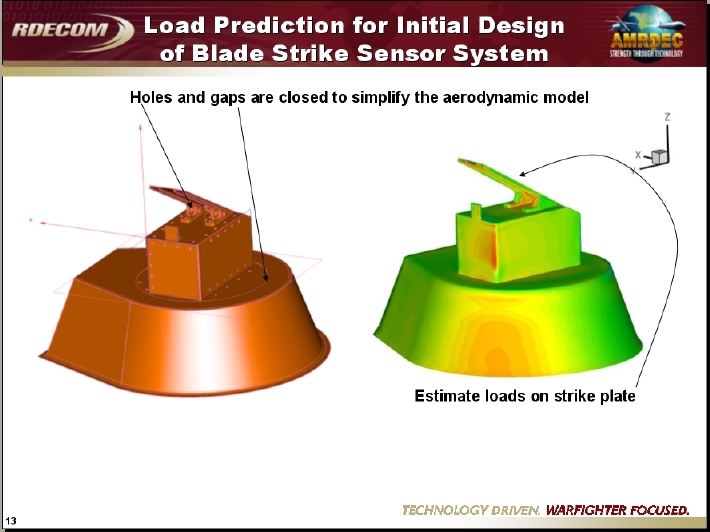
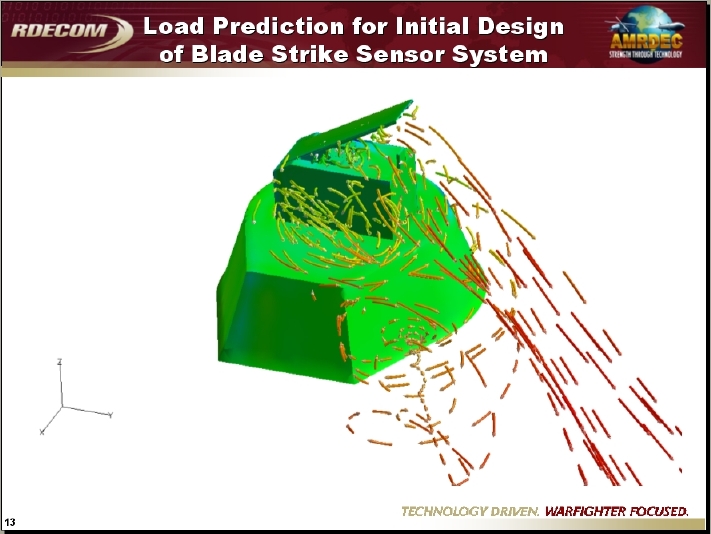
Application #26. Recent applications at AMRDEC
Contributed by Tin-Chee Wong and Dave O’Brien, AMRDEC









NASA Official: David P. Lockard
Contact: FUN3D-support@lists.nasa.gov
Page Last Modified: 2024-04-25 10:30:27 -0400
NASA Privacy Statement
Accessibility
This material is declared a work of the U.S. Government and is not subject to copyright protection in the United States.