Flow Solver Tutorials
Please note that in addition to the tutorials contained here, there are a number of additional resources available in the Training Workshops area of the site. Video footage from approximately 15 in-depth training sessions over a 2-day period are available for viewing. These sessions covered all of the major application areas of FUN3D at the time they were produced.
Flow Solver Tutorial #1
Inviscid flow solve
Intent: Demonstrate simple inviscid execution of the baseline flow solver
This tutorial will describe how to set up and obtain a coarse-grid inviscid flow solution with FUN3D v13.3.
All the grid and input files may be downloaded as described below. Note that the grid for this case is very coarse and is intended for demonstration, rather than accurate aerodynamic analysis. The geometry consists of a stand-alone ONERA M6 (OM6) wing with a symmetry boundary condition imposed at the wing root.
The reader should be familiar with the flow solver inputs (See FUN3D Manual: Appendix B FUN3D Input Files).
Compilation and linking
(See FUN3D Manual: Appendix A Installation).
Files
Download (0.2MB) and gunzip/untar the files:$ tar zvxf flow_demo1.tar.gz x flow_demo1/ x flow_demo1/fun3d.nml x flow_demo1/om6inviscid.fgrid x flow_demo1/om6inviscid.mapbc
The namelist file, fun3d.nml, is used to control the execution
of the solver (initial conditions, physical models, etc.).
The following is a very simple example for basic execution.
There are more aggressive strategies available,
but this will be sufficient to get started.
This example namelist file relies on defaults and only modifies values relevant to this case.
&project
project_rootname = "om6inviscid"
case_title = "OM6 Simple Inviscid Flow Solve Tutorial"
/
&governing_equations
viscous_terms = "inviscid"
/
&reference_physical_properties
mach_number = 0.7
angle_of_attack = 2.0
/
&force_moment_integ_properties
area_reference = 1.067634
x_moment_length = 0.673700
y_moment_length = 1.020000
x_moment_center = 0.168425
/
&nonlinear_solver_parameters
schedule_cfl = 10.0 200.0
/
&code_run_control
steps = 1000
stopping_tolerance = 1.0E-15
restart_write_freq = 1000
restart_read = "off"
/
&raw_grid
grid_format = "fast"
data_format = "ascii"
patch_lumping = "none"
/
Although not necessary,
we will assume that the flow solver executable (nodet or nodet_mpi)
has been installed in your search path to simplify the discussion to follow.
Therefore, we will not reference an explicit path to the executable,
but instead simply invoke directly like any other installed software.
Execute the flow solver
For sequential, i.e., single-processor, execution
the flow solver is invoked as follows,
where the --animation_freq -1 command line option
is specified to provide Tecplot visualization output
for the solid boundary surfaces:
% nodet --animation_freq -1
FUN3D 12.2-63280 started 12/20/2010 at 15:40:12.695 with 1 MPI processes
Contents of file fun3d.nml below------------------------------------------------
&project
project_rootname = "om6inviscid"
[...]
Done.
For parallel (multiple-processor) execution,
the flow solver is invoked through an MPI
command like mpirun, aprun, or mpiexec depending
on your local environment.
It is assumed that your system is configured
for some implementation of MPI
and that all processors have access to the case directory
and to the nodet_mpi executable.
For an OpenMPI-based environment, the run command may look like the following:
% mpirun -machinefile your.machines -np 8 nodet_mpi --animation_freq -1
FUN3D 12.2-63280 started 12/20/2010 at 15:40:12.695 with 8 MPI processes
Contents of file fun3d.nml below------------------------------------------------
&project
project_rootname = "om6inviscid"
[...]
Done.
Post-process the results
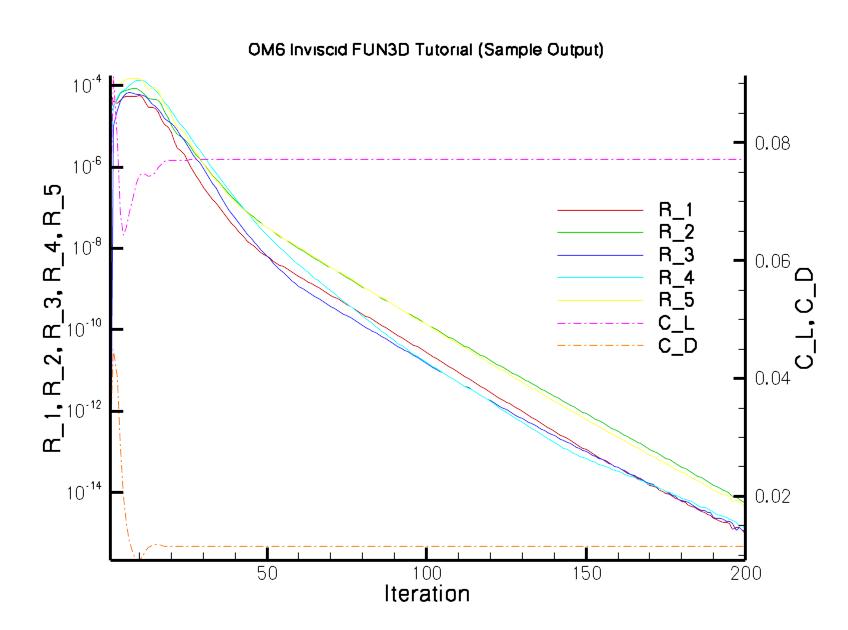
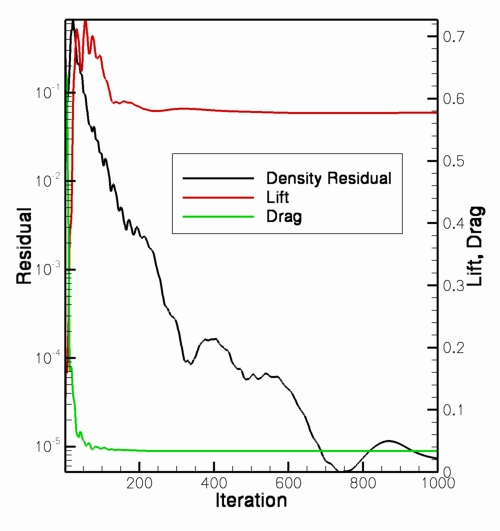
The figure below is a representative convergence history for this case.
The residual information is available in the file om6inviscid_hist.dat
and is in the Tecplot format.
The residual values (R_1, R_2, R_3, R_4, R_5)
represent the convergence of the 5 equations of state
(mass, x-momentum, y-momentum, z-momentum, and energy, respectively).
They are plotted using a Log scale below.
The Tecplot surface visualization file om6inviscid_tec_boundary.dat
is the result of the --animation_freq -1 command line option.
This file contains the primitive variables on each solid boundary surface.
Note: This file may have a .plt or .szplt suffix if your FUN3D is configured
to use the binary Tecplot I/O libraries.
Flow Solver Tutorial #2
Turbulent flow solve
Intent: Demonstrate simple turbulent execution of the baseline flow solver
This tutorial will describe how to set up and obtain a coarse-grid turbulent flow solution with FUN3D v13.3.
All the grid and input files may be downloaded as described below. Note that the grid for this case is very coarse and is intended for demonstration rather than accurate aerodynamic analysis. The geometry consists of a stand-alone ONERA M6 (OM6) wing with a symmetry boundary condition imposed at the wing root.
The reader should be familiar with the flow solver inputs (See FUN3D Manual: Appendix B FUN3D Input Files).
Compilation and linking
(See FUN3D Manual: Appendix A Installation).
Files
Download (1.4MB) and gunzip/untar the files:$ tar zvxf flow_demo2.tar.gz x flow_demo2/ x flow_demo2/fun3d.nml-initial x flow_demo2/fun3d.nml-restart x flow_demo2/om6viscous_symmetry.fgrid x flow_demo2/om6viscous_symmetry.mapbcAs for the first flow solver tutorial, a namelist file,
fun3d.nml, is used to control the execution of the solver
(initial conditions, physical models, etc.).
In this tutorial, we will run the code twice: once to initialize
the flow and a second time to converge the solution to machine precision.
For the first phase,
cp fun3d-nml-initial fun3d.nmlwhich sets up a bare bones example for basic execution:
&project
project_rootname = "om6viscous_symmetry"
case_title = "OM6 Simple Turbulent Flow Solve Tutorial"
/
&reference_physical_properties
temperature_units = "Rankine"
mach_number = 0.7
reynolds_number = 3000000.0
temperature = 460.0
angle_of_attack = 2.0
/
&force_moment_integ_properties
area_reference = 1.067634
x_moment_length = 0.673700
y_moment_length = 1.020000
x_moment_center = 0.168425
/
&nonlinear_solver_parameters
schedule_cfl = 10.0 200.0
schedule_cflturb = 1.0 20.0
/
&code_run_control
steps = 1000
stopping_tolerance = 1.0E-15
restart_write_freq = 1000
restart_read = "off"
/
&raw_grid
grid_format = "fast"
data_format = "ascii"
patch_lumping = "none"
/
Although not necessary,
we will assume that the flow solver executable (nodet or nodet_mpi)
has been installed in your search path to simplify the discussion to follow.
Therefore, we will not reference an explicit path to the executable,
but instead simply invoke directly like any other installed software.
Execute the flow solver
For sequential, i.e., single-processor, execution
the flow solver is invoked as follows,
where the --animation_freq -1 command line option
is specified to provide Tecplot visualization output
for the solid boundary surfaces:
% nodet --animation_freq -1
FUN3D 12.2-63280 started 12/20/2010 at 15:40:12.695 with 1 MPI processes
Contents of file fun3d.nml below------------------------------------------------
&project
project_rootname = "om6viscous_symmetry"
[...]
Done.
For parallel (multiple-processor) execution,
the flow solver is invoked through an MPI
command like mpirun, aprun, or mpiexec depending
on your local environment.
It is assumed that your system is configured
for some implementation of MPI
and that all processors have access to the case directory
and to the nodet_mpi executable.
For an OpenMPI-based environment, the run command may look like the following:
% mpirun -machinefile your.machines -np 8 nodet_mpi --animation_freq -1
FUN3D 12.2-63280 started 12/20/2010 at 15:40:12.695 with 8 MPI processes
Contents of file fun3d.nml below------------------------------------------------
&project
project_rootname = "om6viscous_symmetry"
[...]
Done.
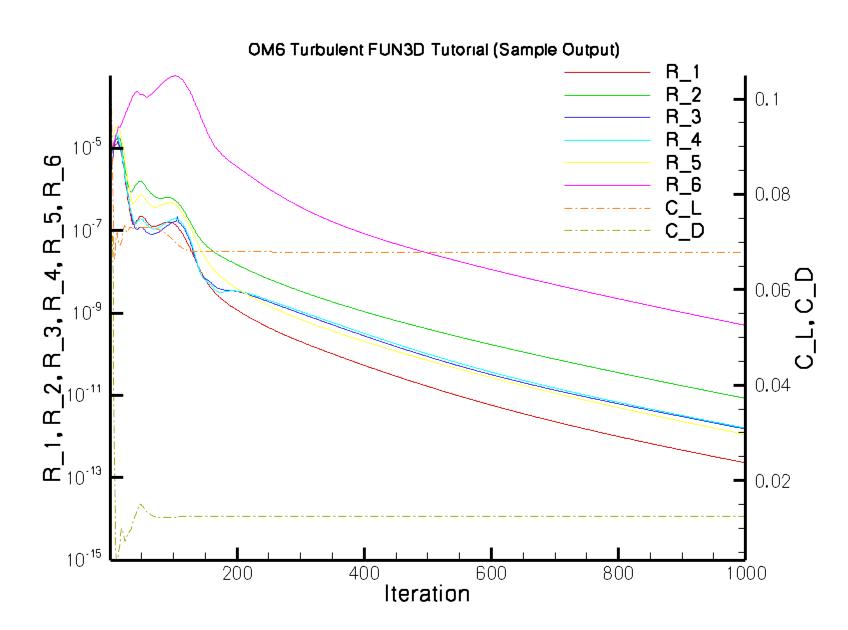
The resulting convergence history is shown in the following plot.
While overall convergence is good, we will restart the solution to continue to converge the solution to machine precision. For this we will need to modify the FUN3D namelist input filefun3d.nml.
The modifications include:
(1) Changing the CFL schedules (nonlinear_solver_parameters namelist
variables schedule_cfl and schedule_cflturb)
since the values were ramped to their maximum values during the initial run;
and
(2) Restarting the solution
(code_run_control namelist variable restart_read).
Note that the restart will run another 1,000 steps
unless the density residual falls below the given threshold (1.0e-15).
The tarball contains this modified fun3d.nml file; so
cp fun3d.nml-restart fun3d.nmlwhich should contain the following:
&project
project_rootname = "om6viscous_symmetry"
case_title = "OM6 Simple Turbulent Flow Solve Tutorial"
/
&reference_physical_properties
angle_of_attack = 2.0
mach_number = 0.7
reynolds_number = 3000000.0
temperature = 460.0
temperature_units = "Rankine"
/
&force_moment_integ_properties
area_reference = 1.067634
x_moment_length = 0.673700
y_moment_length = 1.020000
x_moment_center = 0.168425
/
&nonlinear_solver_parameters
schedule_cfl = 200.0 200.0
schedule_cflturb = 20.0 20.0
/
&code_run_control
steps = 1000
stopping_tolerance = 1.0E-15
restart_write_freq = 1000
restart_read = "on"
/
&raw_grid
grid_format = "fast"
data_format = "ascii"
patch_lumping = "none"
/
Execution of the flow solver using the above FUN3D namelist is
conducted in the same manner as for the initial invocation.
For example, parallel execution is invoked through mpirun as before.
% mpirun -machinefile your.machines -np 8 nodet_mpi --animation_freq -1
FUN3D 12.2-63280 started 12/20/2010 at 15:40:12.695 with 8 MPI processes
Contents of file fun3d.nml below------------------------------------------------
&project
project_rootname = "om6viscous_symmetry"
[...]
Done.
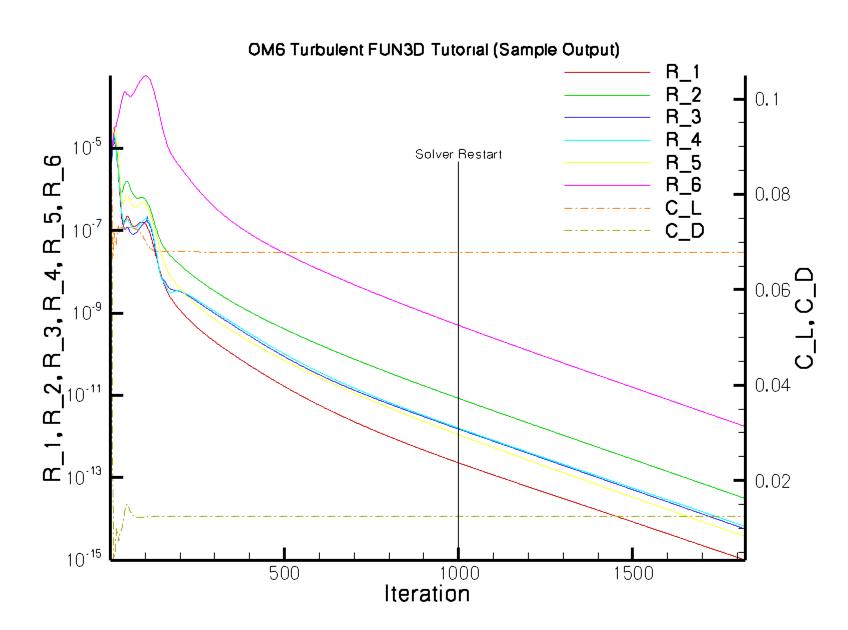
Post-process the results
The following is a representative convergence history for this case.
The residual information is available in the file om6viscous_symmetry_hist.dat
and is in the Tecplot format.
The residual values (R_1, R_2, R_3, R_4, R_5, R_6) represent
the convergence of the 5 equations of state
(mass, x-momentum, y-momentum, z-momentum, energy,
and the 1 Eqn. SA model respectively).
They are plotted using a Log scale below.
The result of the above execution will also generate
the Tecplot file om6viscous_symmetry_tec_boundary.dat
for examination of solid surface quantities.
Flow Solver Tutorial #3
Merge VGRID mesh into mixed elements and run solution
Intent: Demonstrate how to merge tetrahedral VGRID mesh into mixed elements and run turbulent flow solution
This tutorial will describe how to merge a tetrahedral VGRID mesh into mixed elements and execute a turbulent flow solve using FUN3D v13.3.
The grid and input files for this example are from the AIAA DPW-2 workshop and can be downloaded as described below. Note that the grids for this case are very coarse and are intended for demonstration rather than accurate aerodynamic analysis. The geometry consists of a wing-body configuration with half-plane symmetry.
The reader should be familiar with the flow solver inputs (See FUN3D Manual: Appendix B FUN3D Input Files).
Compilation and linking
(See FUN3D Manual: Appendix A Installation).
Files
Download (68MB) and gunzip/untar:$ tar zvxf flow_demo3.tar.gz x flow_demo3/ x flow_demo3/f6wbnc.bc x flow_demo3/f6wbnc.cogsg x flow_demo3/f6wbnc.mapbc x flow_demo3/f6wbnc.poin1 x flow_demo3/fun3d.nml
Note that you need the .poin1 file for merging the grid—normally
this file is not required to process the raw tetrahedral grid.
As with previous flow solver tutorials,
a fun3d.nml namelist file is used to control the execution of the solver
(initial conditions, physical models, etc.).
The following is a very simple example for illustrative purposes;
more advanced strategies are available but not covered here.
&project
project_rootname = "f6wbnc.merged"
case_title = "Merged DPW-2 Tutorial"
/
&reference_physical_properties
angle_of_attack = 1.0
mach_number = 0.75
reynolds_number = 21246.5
temperature = 460.0
temperature_units = "Rankine"
/
&force_moment_integ_properties
area_reference = 72700.0
x_moment_length = 141.200
y_moment_length = 585.647
x_moment_center = 504.900
/
&nonlinear_solver_parameters
schedule_cfl = 10.0 200.0
schedule_cflturb = 1.0 30.0
/
&code_run_control
steps = 1000
stopping_tolerance = 1.0E-15
restart_write_freq = 1000
restart_read = "off"
/
&raw_grid
grid_format = "aflr3"
data_format = "stream"
patch_lumping = "none"
/
&boundary_output_variables
number_of_boundaries = -1 ! compute the number from the following
boundary_list = '6-49'
/
Although not necessary,
we will assume that the utility code vgrid_merge_into_prisms executable
and flow solver executable (nodet or nodet_mpi)
have been installed in your search path to simplify the discussion to follow.
Therefore, we will not reference an explicit path to the executable,
but instead simply invoke directly like any other installed software.
Pre-process the mesh
The first step is to use vgrid_merge_into_prisms to merge
the native tetrahedral VGrid mesh into mixed elements.
Do this by executing vgrid_merge_into_prisms:
% vgrid_merge_into_prisms
enter project name
f6wbnc
f6wbnc.cogsg opening
f6wbnc.cogsg opening 0
f6wbnc.cogsg read header
inew, nc, npo, nbn, npv, nev, t
-1 6558758 1121301 38879 674338 3826019
0.000000000000000E+000
f6wbnc.cogsg nodes 1121301
f6wbnc.cogsg cells 6558758
f6wbnc.cogsg rewind
f6wbnc.cogsg allocate c2n
f6wbnc.cogsg allocate xyz
f6wbnc.cogsg read header,c2n,x,y,z
f6wbnc.cogsg close
f6wbnc.bc opening
f6wbnc.bc read header
f6wbnc.bc faces 77754
f6wbnc.bc allocate faces
f6wbnc.bc read faces
f6wbnc.bc close
f6wbnc n2c
f6wbnc n2c-1
f6wbnc n2c-2
f6wbnc c2e
f6wbnc eptr 7718935
f6wbnc nbound 7718935
f6wbnc bound 1 ntri 186
f6wbnc bound 2 ntri 202
f6wbnc bound 3 ntri 456
f6wbnc bound 4 ntri 237
f6wbnc bound 5 ntri 237
f6wbnc bound 6 ntri 267
f6wbnc bound 7 ntri 367
f6wbnc bound 8 ntri 570
f6wbnc bound 9 ntri 1155
f6wbnc bound 10 ntri 374
f6wbnc bound 11 ntri 1420
f6wbnc bound 12 ntri 1228
f6wbnc bound 13 ntri 81
f6wbnc bound 14 ntri 147
f6wbnc bound 15 ntri 12
f6wbnc bound 16 ntri 11
f6wbnc bound 17 ntri 672
f6wbnc bound 18 ntri 2226
f6wbnc bound 19 ntri 220
f6wbnc bound 20 ntri 1104
f6wbnc bound 21 ntri 2694
f6wbnc bound 22 ntri 7895
f6wbnc bound 23 ntri 4067
f6wbnc bound 24 ntri 202
f6wbnc bound 25 ntri 473
f6wbnc bound 26 ntri 3907
f6wbnc bound 27 ntri 365
f6wbnc bound 28 ntri 430
f6wbnc bound 29 ntri 363
f6wbnc bound 30 ntri 361
f6wbnc bound 31 ntri 792
f6wbnc bound 32 ntri 844
f6wbnc bound 33 ntri 790
f6wbnc bound 34 ntri 509
f6wbnc bound 35 ntri 607
f6wbnc bound 36 ntri 908
f6wbnc bound 37 ntri 4837
f6wbnc bound 38 ntri 4168
f6wbnc bound 39 ntri 1985
f6wbnc bound 40 ntri 291
f6wbnc bound 41 ntri 164
f6wbnc bound 42 ntri 166
f6wbnc bound 43 ntri 291
f6wbnc bound 44 ntri 441
f6wbnc bound 45 ntri 26535
f6wbnc bound 46 ntri 884
f6wbnc bound 47 ntri 990
f6wbnc bound 48 ntri 592
f6wbnc bound 49 ntri 31
f6wbnc fill f2ntb
f6wbnc bound 1 nnode 114
f6wbnc bound 2 nnode 122
f6wbnc bound 3 nnode 257
f6wbnc bound 4 nnode 142
f6wbnc bound 5 nnode 142
f6wbnc bound 6 nnode 158
f6wbnc bound 7 nnode 213
f6wbnc bound 8 nnode 318
f6wbnc bound 9 nnode 647
f6wbnc bound 10 nnode 218
f6wbnc bound 11 nnode 762
f6wbnc bound 12 nnode 662
f6wbnc bound 13 nnode 55
f6wbnc bound 14 nnode 94
f6wbnc bound 15 nnode 12
f6wbnc bound 16 nnode 11
f6wbnc bound 17 nnode 381
f6wbnc bound 18 nnode 1182
f6wbnc bound 19 nnode 133
f6wbnc bound 20 nnode 619
f6wbnc bound 21 nnode 1475
f6wbnc bound 22 nnode 4117
f6wbnc bound 23 nnode 2157
f6wbnc bound 24 nnode 122
f6wbnc bound 25 nnode 270
f6wbnc bound 26 nnode 2094
f6wbnc bound 27 nnode 213
f6wbnc bound 28 nnode 246
f6wbnc bound 29 nnode 209
f6wbnc bound 30 nnode 206
f6wbnc bound 31 nnode 434
f6wbnc bound 32 nnode 460
f6wbnc bound 33 nnode 437
f6wbnc bound 34 nnode 284
f6wbnc bound 35 nnode 335
f6wbnc bound 36 nnode 539
f6wbnc bound 37 nnode 2520
f6wbnc bound 38 nnode 2197
f6wbnc bound 39 nnode 1063
f6wbnc bound 40 nnode 293
f6wbnc bound 41 nnode 166
f6wbnc bound 42 nnode 168
f6wbnc bound 43 nnode 293
f6wbnc bound 44 nnode 247
f6wbnc bound 45 nnode 13449
f6wbnc bound 46 nnode 498
f6wbnc bound 47 nnode 554
f6wbnc bound 48 nnode 347
f6wbnc bound 49 nnode 25
f6wbnc.mapbc opening
f6wbnc.mapbc read header
f6wbnc bound 1 ibc 5050
f6wbnc bound 2 ibc 5050
f6wbnc bound 3 ibc 5050
f6wbnc bound 4 ibc 5050
f6wbnc bound 5 ibc 5050
f6wbnc bound 6 ibc 4000
f6wbnc bound 7 ibc 4000
f6wbnc bound 8 ibc 4000
f6wbnc bound 9 ibc 4000
f6wbnc bound 10 ibc 4000
f6wbnc bound 11 ibc 4000
f6wbnc bound 12 ibc 4000
f6wbnc bound 13 ibc 4000
f6wbnc bound 14 ibc 4000
f6wbnc bound 15 ibc 4000
f6wbnc bound 16 ibc 4000
f6wbnc bound 17 ibc 4000
f6wbnc bound 18 ibc 4000
f6wbnc bound 19 ibc 4000
f6wbnc bound 20 ibc 4000
f6wbnc bound 21 ibc 4000
f6wbnc bound 22 ibc 4000
f6wbnc bound 23 ibc 4000
f6wbnc bound 24 ibc 4000
f6wbnc bound 25 ibc 4000
f6wbnc bound 26 ibc 4000
f6wbnc bound 27 ibc 4000
f6wbnc bound 28 ibc 4000
f6wbnc bound 29 ibc 4000
f6wbnc bound 30 ibc 4000
f6wbnc bound 31 ibc 4000
f6wbnc bound 32 ibc 4000
f6wbnc bound 33 ibc 4000
f6wbnc bound 34 ibc 4000
f6wbnc bound 35 ibc 4000
f6wbnc bound 36 ibc 4000
f6wbnc bound 37 ibc 4000
f6wbnc bound 38 ibc 4000
f6wbnc bound 39 ibc 4000
f6wbnc bound 40 ibc 4000
f6wbnc bound 41 ibc 4000
f6wbnc bound 42 ibc 4000
f6wbnc bound 43 ibc 4000
f6wbnc bound 44 ibc 4000
f6wbnc bound 45 ibc 6662
f6wbnc bound 46 ibc 4000
f6wbnc bound 47 ibc 4000
f6wbnc bound 48 ibc 4000
f6wbnc bound 49 ibc 4000
f6wbnc.poin1 nodes 38879 674338
f6wbnc.poin1 nodes 38879 674338
Line breaks found in .poin1 info: 6
........resulting points missed : 6
Condensed from .poin1 info: n_lines= 25104
..maximum number of points in lines= 31
..minimum number of points in lines= 22
..average number of points in lines= 26.6480640535373
....total number of points in lines= 668973
Max layers in poin1 file: 31
Min layers in poin1 file: 22
Layers unmerged: 2
Pass Number 1
Number of splayed-open cells requiring Steiner points = 0
Number of tet-fans requiring Steiner points = 2433
Number of pyramid conflicts requiring Steiner points = 0
Searching for faces on boundary 1 of 49
Searching for faces on boundary 10 of 49
Searching for faces on boundary 20 of 49
Searching for faces on boundary 30 of 49
Searching for faces on boundary 40 of 49
Done merging prism stacks:
Before/after merging, number of nodes = 1121301 1123718
Before/after merging, number of tets = 6558758 3039656
Before/after merging, number of pyrs = 0 7337
Before/after merging, number of przs = 0 1172171
Before/after merging, number of tris = 77754 62166
Before/after merging, number of quads = 0 7794
Writing stream mixed element grid...
Opening VGRID family info...filename=f6wbnc.mapbc
Merging procedure produced 3 files as below:
f6wbnc.merged.b8.ugrid
f6wbnc.merged.mapbc
f6wbnc.merged.lines_fmt
Note f6wbnc.merged.mapbc contains family info.
Note f6wbnc.merged.lines_fmt contains implicit line info.
The program will merge the grid and dump some statistics to the screen.
In this case,
the number of tetrahedra was reduced from 6,558,758 to 3,039,656
while 1,172,171 prisms and 7,337 pyramids were introduced.
The total number of nodes in the mesh went from 1,121,301 to 1,123,718.
The result of the merging process is a stream AFLR3 .b8.ugrid file
with the same project name as the original grid
but with a .merged extension.
It is advised that you do not change this new appended project name.
Execute the flow solver
You can now execute the flow solver as usual, e.g.,
% mpirun -machinefile your.machines -np 32 nodet_mpi --animation_freq -1
The resulting convergence history is represented in the following plot.
You may also view the resulting f6wbnc.merged_tec_boundary.dat file
with Tecplot.
Zooming in on the symmetry plane,
you will see that the triangular faces have become quad faces,
indicating that the boundary layer grid now consists of prismatic elements.
NASA Official: David P. Lockard
Contact: FUN3D-support@lists.nasa.gov
Page Last Modified: 2024-05-02 17:12:16 -0400
NASA Privacy Statement
Accessibility
This material is declared a work of the U.S. Government and is not subject to copyright protection in the United States.